앞에서 우리는 하나의 집단에 대한 모집단의 평균을 검증하기 위해 신뢰구간을 구하고, 가설검증을 해보았다.
-> (one-sample-test)
이제는 2개의 집단이 존재하고, 집단의 평균이 통계적으로 유의미한지 비교하는 상황을 생각해보자.
-> (two sample-test)
두 모집단 비교
- 앞에서 진행한 one-sample-test와는 다르게, 두 집단을 비교할때 두 집단의 모분산이 동일한가?(equal variance) 동일하지 않는가?(unequal variance)에 따라 검증 수행 방법이 달라진다. 따라서 two-sample-test를 진행하기 전에 등분산 검정을 먼저 수행한다.
- 그리고 한 표본의 값이 다른 표본의 값에 영향을 주는지에 따라서 (두 표본이 독립적인가?) 에 따라서 independent sample t-test와 dependent sample t-test로 나뉜다. 우선 표본이 서로 독립적인 경우부터 보자.
표본이 독립적인 경우

어디서 많이 본것 같지 않는가? 표본분포를 구할 때, 진행한 작업과 똑같다.
서울대와 연세대 두 집단에서 수학 점수의 평균을 100명의 샘플을 통해 구해서 그 차이를 구한다.
| Sample | Xabar-Xbbar |
| SampleA - SampleB(1) | 10 |
| SampleA - SampleB(2) | 5 |
| SampleA - SampleB(3) | 15 |
| ... | ... |
이렇게 각 두 집단에서 100명으로 만들 수 있는 모든 종류의 샘플을 만들었다고 가정해보자. 이렇게 만들어진 각 샘플의 평균값의 분포(10,5,15)들로 이루어진 이론상의 분포를 표본분포(Sampling distribution)이라고 한다.
- 이렇게 만들어진 Xabar-Xbbar는, 두 모집단이 정규분포인 경우 정규분포임.
- 두 모집단이 정규분포가 아닌 경우, Xabar-Xbbar n>30 일때, 근사적으로 정규분포임
- Xabar-Xbbar의 표본분포의 평균은 u_1-u_2
- Xabar-Xbbar의 표본분포의 분산은 α_2^2/n_1 + α_2^2/n_2
이제 Xabar-Xbbar의 표본분포를 표준화 시키자. 그럼 아래의 그림을 얻을 수 있음.
$$
Z=\frac{\left(\bar{x}_{1}-\bar{x}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}
$$
이제 Z-score를 이용하여, Xabar-Xbbar에 대한 가설검정과 신뢰구간을 구할 수 있을 것이다.
여기서 one-sample-test와는 다르게, 두 집단을 비교할때 두 집단의 모분산이 동일한가?(equal variance) 동일하지 않는가?(unequal variance)에 따라 검증 수행 방법이 달라진다라고 하였음.
F-test
이분산인가, 등분산인가를 검증하기 위해 F-test를 사용함. 두 분산이 같다는 가설을 검증하여, 귀무가설을 기각한다면 이분산, 기각하지 못한다면 등분산임.
$$
\text { Ho: } \sigma_{1}^{2}=\sigma_{2}^{2} \text { or Ho: } \sigma_{1}^{2} / \sigma_{2}^{2}=1
$$
분산을 검정하기 위해 F-분포의 F-value를 이용하여 검증
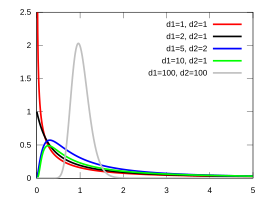
$$
\text { F Value }=\frac{\text { Larger Sample Variance }}{\text { Smaller Sample Variance }}=\frac{\sigma 1^{2}}{\sigma 2^{2}}
$$
- 예시. 이분산 가정을 검정하라
- n_1=31,n_2=41, S_1=105.96,S_2=36.42
- F-value=105.96 / 36.42 = 2.91 / 자유도 : df_1 = (31-1) 30 , df_2=(41-1) 40
- F-table을 참고하여 가설검증
- 1% 유의수준에서 F critical value = 2.20
- F=2.91>2.20 두 집단의 분산이 같다는 가설을 기각
- http://www.socr.ucla.edu/Applets.dir/F_Table.html
표본이 독립적인 경우/ 등분산
F-test를 진행하였을 때, 귀무가설을 기각하지 못해 두 집단이 등분산임을 가정하고 진행해보자. 등분산이라면, 다음과 같은 식일 것임.
$$
\begin{aligned}
&\text { If } \sigma_{1}^{2}=\sigma_{2}^{2} \\
&Z=\frac{\left(\bar{x}_{1}-\bar{x}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{\sigma^{2}}{n_{1}}+\frac{\sigma^{2}}{n_{2}}}}=\frac{\left(\bar{x}_{1}-\bar{x}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\sigma^{2}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}}
\end{aligned}
$$
여기서 현실적으로 두 모집단의 분산인 α^2은 알기가 어려움. 따라서 t 통계량을 이용하여 가설검정을 수행함. 이때 자유도는 (n1+n2) - 2임
$$
\begin{aligned}
&t=\frac{\left(\bar{X}_{1}-\bar{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{S_{p}^{2}\left(\frac{1}{n_{1}}+\frac{1}{n_{2}}\right)}} \\
&\text { d.f. }=n_{1}+n_{2}-2
\end{aligned}
$$
여기서 S_p^2는 통합분산(pooled variance)으로 두 표본에서 도출한 분산의 평균개념으로 생각하면 된다.
$$
s_{p}^{2}=\frac{\left(n_{1}-1\right) s_{1}^{2}+\left(n_{2}-1\right) s_{2}^{2}}{n_{1}+n_{2}-2}
$$
표본이 독립적인 경우/ 이분산
F-test를 진행하였을 때, 귀무가설을 기각하여 두 집단이 이분산임을 가정하고 진행해보자.
$$
t=\frac{\left(\bar{X}_{1}-\bar{X}_{2}\right)-\left(\mu_{1}-\mu_{2}\right)}{\sqrt{\frac{S_{1}^{2}}{n_{1}}+\frac{S_{2}^{2}}{n_{2}}}}
$$
t-value는 위 그림과 같이 구하고, 자유도는 아래의 식처럼 구하여 가설검정 진행
$$
\text { d.f. }=\frac{\left(s_{1}^{2} / n_{1}+s_{2}^{2} / n_{2}\right)^{2}}{\frac{\left(s_{1}^{2} / n_{1}\right)^{2}}{n_{1}-1}+\frac{\left(s_{2}^{2} / n_{2}\right)^{2}}{n_{2}-1}}
$$
표본이 독립이지 않는 경우
dependent sample t-test(Paired t-test)는 Paired된 관계에서 전후 차이가 있는지 없는지 보는 것이다.
대표적으로 사전 사후 관계를 보는것이 있다. 같은 조사대상에게 신약을 개발 후, 개발 전 상태를 체크하고, 약을 투입 후 상태를 체크하여 두 쌍을 비교하는 것이다.
신약 복용 후 집단은 신약 복용 전 집단과 연관되어있기 때문에 독립이 아니며, 짝을 이루기 때문에 paired sample이라고 함
| 독립표본 t 검정 | 대응표본 t 검정 |
| 조사대상 개체가 다름 | 조사대상 개체가 같음 |
| 두 범주의 표본숫자가 다를 수 있음 | 표본 숫자가 같음 |
| 다른 집단을 비교 | 전후 개념이 있는 경우가 많음 |
출처:R을 이용한 누구나 하는 통계분석. 안재형 지음 | 한나래
- Paired t-test는 같은 조사대상에게 실험을 진행하기 때문에 표본 숫자가 같다. 따라서 F-test로 등분산성을 검증할 필요가 없다.
- 반대로 표본이 독립일 경우 샘플 수가 다를 수 있기 때문에 F-test를 진행하여 이분산인지 등분산인지 검증하는 것이다.
| X_1 | X_2 | d=difference |
| 25 | 25 | 0 |
| ... | ... | .. |
| X_1 bar | X_2bar | d_bar |
이렇게 X_1와 X_2의 차이를 differnece라고 하고, 이 difference의 차이의 평균을 D_bar라고 하자.
차이에 대한 평균과 , 분산을 아래와 같이 구할 수 있다.
$$
\bar{D}=\frac{\sum_{i=1}^{n}\left(X_{A, i}-X_{B, i}\right)}{n}, S_{D}=\sqrt{\frac{\sum_{i=1}^{n}\left(X_{A, i}-X_{B, i}-\bar{D}\right)^{2}}{n-1}}
$$
위에서 구한 평균과 분산을 통해 t-value를 아래와 같이 구하여 t-test를 진행할 수 있다. d_0은 연구자에 따라서 차이가 없음을 나타내는 0으로 둘 수도 있다. 여기서 자유도는 n-1이다.
$$
T=\frac{\bar{D}-d_{0}}{S_{D} / \sqrt{n}}
$$
이전 포스트에서 가설검정을 진행한것과 같이 설정한 유의수준에서 두 대응표본의 차이가 있으면 위 식에서 도출한 t-value의 절대값이 설정한 유의수준에 따른 t-critical value보다 클것이다. 이를 통해 두 표본의 차이가 있는지 검증할 수 있다.
'블로그 > Statistics & Math' 카테고리의 다른 글
| [비모수 통계] KS test (Kolmogorov–Smirnov test) 방법 (0) | 2022.06.30 |
|---|---|
| [기초 통계] 08. 모비율 검정(One sample case) (0) | 2022.06.29 |
| [기초 통계] 06. 가설검증과 오류 (0) | 2022.06.01 |
| [기초 통계] 05. 구간추정과 신뢰구간 (0) | 2022.06.01 |
| [기초 통계] 04. 표본 분포와 특징 (0) | 2022.06.01 |

