시계열 데이터에서 가장 먼저 그려야 할 것은 바로 시간 그래프(Time plot)이다.
즉, 관측값을 관측 시간에 따라 직선으로 연결한 그래프이다.
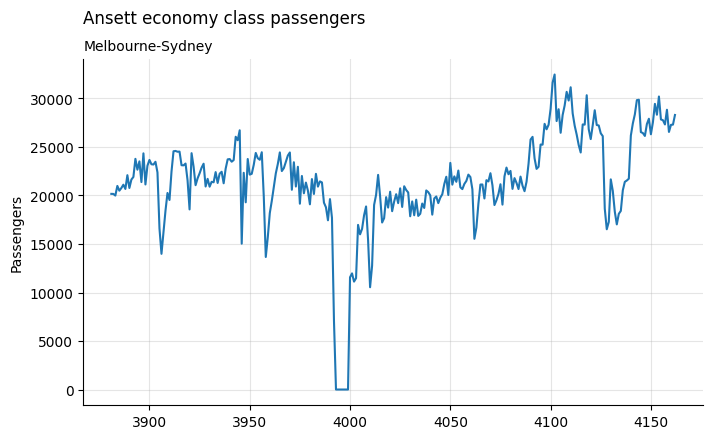
위 그래프는 아래와 같은 특징을 보여준다.
- 1989년은 파업으로 인하여 수송객이 없었던 기간 (3980 인덱스)
- 1992년은 수송객이 감소했던 기간이며, 이코노미 좌석이 비즈니스 좌석으로 교체 되었음 (4120-4140 인덱스)
- 1991년 후반에는 소송객이 크게 증가했다 (4050 이후)
- 관측값이 없는 일부 기간이 있음 (4000 전)
효과적으로 미래 승객수를 예측하기 위해서는 그래프에서 나타나는 이러한 특징을 전부 모델에서 고려해야 한다.
아래는 호주 당뇨병 약 월별 매출에 대한 시계열 그래프이다.

분명하게 증가하는 추세를 확인할 수 있으며, 계절성 패턴의 크기가 뚜렷하게 증가함. 매년 초마다 의약품 매출이 급감하는데, 이것은 환자들이 연말에 저렴하게 의약품을 비축할 수 있도록 하는 정부의 보조금 정책때문임.
시계열의 패턴을 파악하기 위해서는 추세(trend)와 계절성(seasonality)를 매우 주의하여 정의해야함.
추세(trend)
: 데이터가 장기적으로 증가하거나 감소할 때, 추세가 존재한다고 할 수 있다. 추세는 선형적일 필요는 없으며, 때때로 어떤 추세가 증가에서 감소로 변화하는 경우에는 추세의 방향이 전환되었다고 언급한다. 위 당뇨병의 약 월별 매출은 증가하는 뚜렷한 추세가 존재한다.
계절성(seasonality)
: 해마다 특정한 때나 1주일마다 특정 요일에 나타나는 계절성 요인이 시계열에 영향을 줄 때, 계절성 패턴이 나타난다.
계절성은 빈도의 형태로 나타나는데, 그 빈도는 항상 일정하며 알려져 있다. 당뇨병 약 월별 매출액에는 계절성이 나타나는데, 이 계절성은 부분적으로 연말에 발생하는 약품 가격 변동에 의한 것이다.
주기성(Cycle)
: 고정된 빈도가 아닌 형태로 증가나 감소하는 모습을 보일 때, 주기가 나타난다. 보통 경제 상황 때문에 일어나고, 흔히 "경기 순환(Business cycle)"과 관련이 있다.
주기적인 패턴과 계절적인 패턴은 다르다. 일정한 빈도로 나타나지 않는 요동은 주기성을 가지고 있다고 한다. 빈도가 변화하지 않고, 연중 어떤 시기와 연관되어 있다면 그 요동은 계절성이라고 한다. 일반적으로는 주기들의 평균 길이가 계절성 패턴보다 길게 나타나며, 주기의 크기는 변동성이 더욱 크다.
예측 모델을 만들때는, 이러한 패턴을 잡아낼 수 있는 기법을 선택할 수 있다. 하지만, 종가의 경우 추세나 계절성 또는 주기적인 요동이 없을 수 있다. 또한, 무작위적인 파동(big jump 등)이 있을 수 있다. 따라서, 주가의 예측은 매우 어려운 시계열 예측 문제가 될 수 있다.
계절성 그래프:
계절성 그래프는 계절에 대한 관측 데이터를 그래프로 나타낸 것이다. 당뇨병 약 매출의 그래프인데, 매년 1월에 매출이 크게 뛴다는 것을 확인할 수 있으며, 2월에는 감소하는 패턴을 확인할 수 있다.

자기 상관
현재의 상태가 과거 그리고 미래의 상태에 밀접한 연관을 지니는 경우를 말한다. 즉, 자기상관(Autocorrelation)은 시계열의 시차 값(lagged values) 사이의 선형 관계를 측정할 수 있다.


r0, r4, r8처럼 고점은 4개의 분기마다 나타나는 경향이 있고, 마찬가지로 저점 역시 4개의 분기마다 나타나는 경향이 있다.
데이터에 추세가 존재할 때, 자기 상관은 큰 양의 값을 갖는 경향이 있는데, 왜냐하면 시간적으로 가까운 관측치들이 비슷하기 때문이다. 그래서 추세가 있는 시계열의 ACF는 양의 값을 갖는 경향을 보이며, 이러한 ACF의 값은 시차가 증가함에 따라 서서히 감소한다.
데이터에 계절성이 존재할 때의 자기상관도 다른 시차의 경우보다 더 크게 나타난다. 왼쪽 그래프의 ACF를 오른쪽에 그려보았다. 이때, 전체적으로 ACF 그래프가 감소하는 것은 추세 때문인 반면에, 주기적으로 줄다가 다시 올라가는 물결모양이 나타나는 것은 계절성이 나타나기 때문이다.


백색잡음(white noise)
: 자기상관이 없는 시계열을 백색잡음이라고 한다. 무작위 적인 값 때문에 자기상관이 정확하게 0은 아니지만, 거의 0에 가까운 값이 나타나며 막대의 95%가 ±2/√에 들어간다 (파란색 영역) - 계절성과 추세가 없음
-> 다른 말로 하면, 이전 시점의 Y값만 가지고 예측하는 모델을 활용하기 어려움. 다른 독립변수 X가 필요함 !


'블로그 > Statistics & Math' 카테고리의 다른 글
| [Time Series] 단순 예측 기법 및 변환, 잔차 진단 (1) | 2024.01.22 |
|---|---|
| [Time Series] Preface to this read-along (1) | 2024.01.22 |
| [ANOVA] One-way ANOVA, ANOVA table (0) | 2022.07.22 |
| [비모수 통계] KS test (Kolmogorov–Smirnov test) 방법 (0) | 2022.06.30 |
| [기초 통계] 08. 모비율 검정(One sample case) (0) | 2022.06.29 |



