머신러닝은 주어진 데이터를 가장 잘 설명하는 '함수'를 찾는 알고리즘을 디자인한 것이다. 그렇다면, 주어진 데이터가 아닌 관측하지 못한 데이터에 대해서 해당 '함수'가 얼마나 정확한 예측을 해낼 수 있을까?
다음과 같은 문제를 일반화 문제라고 하는데, 머신러닝의 목표는 주어진 데이터를 잘 학습하는 optimization이 아니라, 우리가 관측하지 못한 데이터(unseen data)에 대해서 일반화(generalization)하는 것이다.
이러한 일반화를 위해 우리는 실제 확률 분포로부터 샘플링하여 수집된 데이터만을 가지고 " 현상을 가장 잘 설명하는 확률 분포 모델"을 추정함으로써, 우리가 알고 싶은 실제 확률 분포를 근사하게 된다.
이때 주어진 데이터를 잘 추정하기 위해 가능도를 최대화하도록 파라미터를 추정하는것을 MLE(Maximum Likelihood Estimation)라고 한다.
실제 확률 분포가 만약 가우시안 이라면, 추정해야 하는 파라미터 θ는 평균 μ와 분산 σ2이 될것이며, 이항분포면 어떤 시행의 결과가 성공일 확률 P가 될것이다.
예시를 들어보자.
나와 친구와 내기를 했는데 동전을 던졌을 때, 동전의 앞면이 나오면 50원을 받고, 반대인 뒷면이 나오는 경우에는 20원을 내야 하는 내기이다. 나는 게임에 참여할지 결정하기 위해서 100번을 던져 본다. 이때, 나는 앞면이 30번, 뒷면이 70번 나왔다는것을 관측하였다. 한 번 게임을 할 때 마다 얻을 수 있는 수익의 기댓값을 계산해보자.
기댓값은 보상과 그 보상을 받을 확률을 곱한 값의 총합으로 얻을 수있기 때문에 다음과 같이 계산할 수 있다.
\begin{equation}
\begin{aligned}
\mathbb{E}_{\mathrm{x} \sim P}[\text { reward }(\mathrm{x})] &=P(\mathrm{x}=\text { Head }) \times 50+P(\mathrm{x}=\operatorname{Tail}) \times(-20) \\
& \approx \frac{30}{100} \times 50-\left(1-\frac{30}{100}\right) \times 20=15-14=1
\end{aligned}
\end{equation}
우리는 위 과정을 통해 머릿속으로는 이미 MLE를 수행하여 θ(앞면이 나올 확률) 를 추정했는데, 이러한 과정을 이항분포를 활용해 일반화 해보자. 동전을 던지는 사건은 앞면(Head) 또는 뒷면(Tail)로 결과가 나오는 베르누이 분포를 따르며, 여러번 반복 시행하면 이항 분포를 따른다.
\begin{equation}
K \sim \mathcal{B}(n, \theta)
\end{equation}
n= 시행 횟수, θ = 앞면이 나올 확률
따라서, 이항 분포의 파라미터 θ(앞면이 나올 확률)가 있을 때, n번 동전을 던져서 앞면이 k번 나올 확률은 다음과 같이 만들 수 있다.
\begin{equation}
\begin{aligned}
P(K=k) &=\left(\begin{array}{c}
n \\
k
\end{array}\right) \theta^{k}(1-\theta)^{n-k} \\
&=\frac{n !}{k !(n-k) !} \cdot \theta^{k}(1-\theta)^{n-k}
\end{aligned}
\end{equation}
위에서 내가 실제로 동전을 던져서 얻은 데이터에서 우리는 n=100했을 때, 앞면이 30번 나왔다는 것을 확인했다. 따라서 해당 동전을 던졌을 때 앞면에 나오는 확률을 설명하는 θ에 대한 함수는 다음과 같이 구할 수 있다.
\begin{equation}
J(\theta)=\frac{100 !}{30 !(100-30) !} \cdot \theta^{30}(1-\theta)^{100-30}
\end{equation}
이때, θ(앞면이 나올 확률)을 함수에 넣어 얻는 값을 가능도(우도) likelihood라고 하며, 이 함수를 가능도 함수 Likelihood Function이라고 한다.
\begin{equation}
J(\theta)=P(n=100, k=30 \mid \theta)
\end{equation}
θ(앞면이 나올 확률)에 대해서 그래프를 그려보면, 아래와 같으며 동전이 앞면이 나올 확률을 0부터 1까지 0.1 단위로 변화시키면서 가능도를 확인해보면 아래와 같다.
그래프에서 0.3에서 J(θ)이 최대가 되는 것을 알 수 있으며, θ(앞면이 나올 확률)이 0.3일 때 이항 분포는 우리가 관측한 데이터를 가장 잘 재현한다.
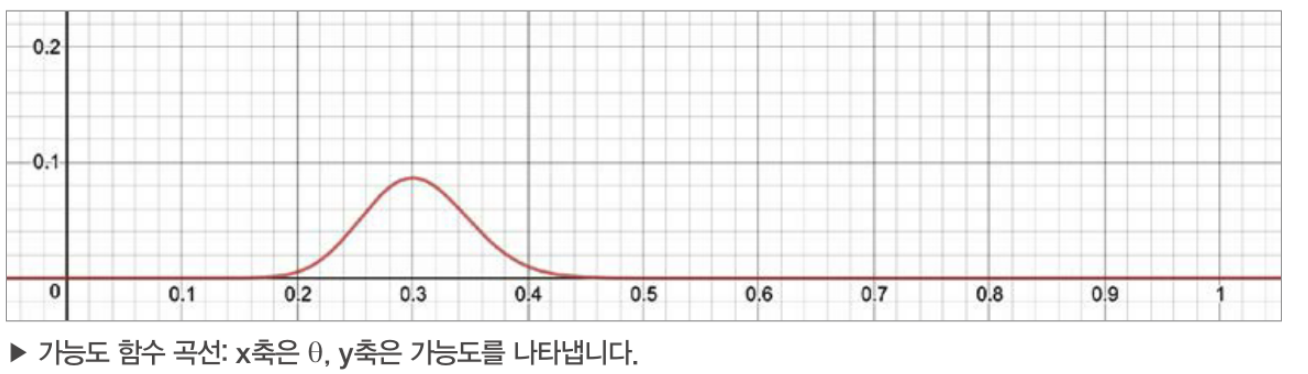
즉, 관측된 데이터를 가장 잘 설명하는 가능도 J(θ)를 최대화하는 θ를 추정하기 때문에 최대가능도 추정(MLE)라고 하는 것이다.
이러한 MLE 과정에서 부터 딥러닝의 손실함수로 활용하는 음의 로그우도(Negative log-likelihood,NLL)를 유도해보자.
알려지지 않은 확률 함수 P 에서 주어진 데이터가 아래와 같을때,
\begin{equation}
x_{1: n}=\left\{x_{1}, x_{2}, \cdots, x_{n}\right\}
\end{equation}
가능도는 위의 데이터를 설명하는 확률 분포 파라미터에 대한 함수로 다음과 같이 표현할 수 있다.
\begin{equation}
P\left(\mathrm{x}=x_{1: n} ; \theta\right)
\end{equation}
서로 독립 i.i.d. (independent and identical distributed) 인 관측치 데이터(x1,x2,x3..xn)에 대한 가능도는 다음과 같이 표현할 수 있다.
\begin{equation}
P\left(x_{1}, x_{2}, \cdots, x_{n} \mid \theta\right)=P\left(x_{1} ; \theta\right) P\left(x_{2} ; \theta\right) \cdots P\left(x_{n} ; \theta\right)=\prod_{i=1}^{n} P\left(x_{i} ; \theta\right)
\end{equation}
여기에 곱셉보다 덧셈이 계산이 간편하기 때문에, 로그를 취하여 곱을 합으로 표현하면 아래와 같이 표현할 수 있다.
\begin{equation}
\log P\left(x_{1}, x_{2}, \cdots, x_{n} \mid \theta\right)=\sum_{i=1}^{n} \log P\left(x_{i} ; \theta\right)
\end{equation}
그리고 위 식에서 -1를 곱해주면 최소화 문제로 치환할 수 있으며, 딥러닝 모델의 손실함수로 활용하는 음의 로그우도(Negative log-likelihood,NLL)로 변경할 수 있다.
\begin{equation}
-\sum_{i=1}^{n} \log P\left(x_{i} ; \theta\right)
\end{equation}
딥러닝을 학습하는 과정도 MLE를 하는 것과 같다고 할 수 있다. 만약 MNIST 분류 문제를 풀고자 한다면 0부터 9까지의 숫자를 분류를 위한 멀티눌리 분포로 생각할 수 있다. 만약 음의 로그우도(Negative log likelihood)를 Loss로 사용하면 가능도 J(θ)는 음의 로그우도이며, J(θ)를 최소화 하는 Weight parameter θ를 찾아내기 위해 경사하강법(Gradient descent)를 이용하여 학습하기 때문이다.
Reference : 김기현의 자연어처리 딥러닝 캠프
'블로그 > 딥러닝' 카테고리의 다른 글
| [RAG] RAG 성능 향상을 위한 Re-ranking (1) | 2024.07.11 |
|---|---|
| 딥러닝의 과대적합(Overfitting)을 해결하자 (0) | 2023.04.24 |
| 단층에서부터 Deep한 다층 퍼셉트론까지(Universal Approximation Theorem) (0) | 2022.08.13 |
| [이상치 탐지] 금형 센서 데이터 이상 탐지 사례 (0) | 2022.07.06 |
| 역전파 알고리즘(Back Propagation)과 Delta Rule(1) (0) | 2022.07.06 |



