딥러닝 아키텍처가 도대체 어떻게 데이터를 "학습"하고 그렇게 어려운 문제를 해결할 수 있는가?라고 했을 때, 그 핵심이 되는 알고리즘은 "역전파 알고리즘(Back Propagation)"이라고 할 수 있다.
과적합, Vanishing gradient 등과 같은 명백한 단점이 존재하여 역전파 알고리즘(Back Propagation)의 단점을 보안하려는 연구가 계속되고 있음에도 불구하고, 여전히 많은 딥러닝 아키텍처는 역전파 알고리즘을 기반으로 데이터를 "학습"한다.
역전파 알고리즘(Back Propagation)
모델의 출력값과 기댓값을 비교하여 차이(오차)를 줄여나가는 방향으로 Weight update를 하고, 상위층에서 역전파하여 하위층에서 이를 근거로 다시 weight를 업데이트하는 것
상위층인 출력층과 하위층인 입력층의 방향으로 출력값과 기댓값의 차이인 Error를 역(Back)의 방향으로 전파하면서 가중치를 업데이트하기 때문에 역전파 알고리즘(Back Propagation)이라고 한다.
개인적으로 딥러닝을 배우기전에 역전파 알고리즘을 제대로 배워야 한다고 생각하는데, 그 이유는 가장 기본적인 DNN, Vision에서 활용된 CNN, 시퀀셜을 반영한 RNN 모두 역전파 알고리즘을 동작원리로 채택하고 있기 때문이다. 그렇다면 역전파 알고리즘을 알아보기 전에, 역전파 알고리즘의 가장 간단한 버전인 Delta Rule에 대해서 알아보자.
델타 룰(Delta Rule) , Perceptron learning rule
Delta Rule은 입출력 함수가 선형의 Unit으로 이루어진 신경망에 대하여 모든 입력 값으로부터 얻어지는 출력 값과 정답과의 오차의 제곱의 총합을 최소로 하도록 Weight을 조정하는 것
- Hidden layer는 없이 input layer*와 output layer로만 구성되어 있으며, Linear activation function만을 활용한 하나의 신경망을 생각해보자.
*참고: 입력 벡터 x를 제공하는 부분을 input layer라고 부르는 것은 논란의 여지가 있다. input layer는 독립적인 퍼셉트론 열에서 생성하는 것이 아니라, 학습 데이터로부터 얻어져 직접 output layer, 혹은 hidden layer에 제공되기 때문이다(윤덕호, 파이썬 날코딩으로 알고 짜는 딥러닝(2019). 본 포스팅에서는 이해의 편의성을 위해 input layer라고 지칭하겠음
아래 그림에서 O1,O2은 각 Input 데이터에 Weight 가중치를 곱하고 Bias를 더한 값이다. 그럼 실제 값(t1,t2)와의 차이인 오차를 구할 수 있을 것이고, 이 오차를 최소화하는 Weight 값을 업데이트 할 수 있을 것이다.
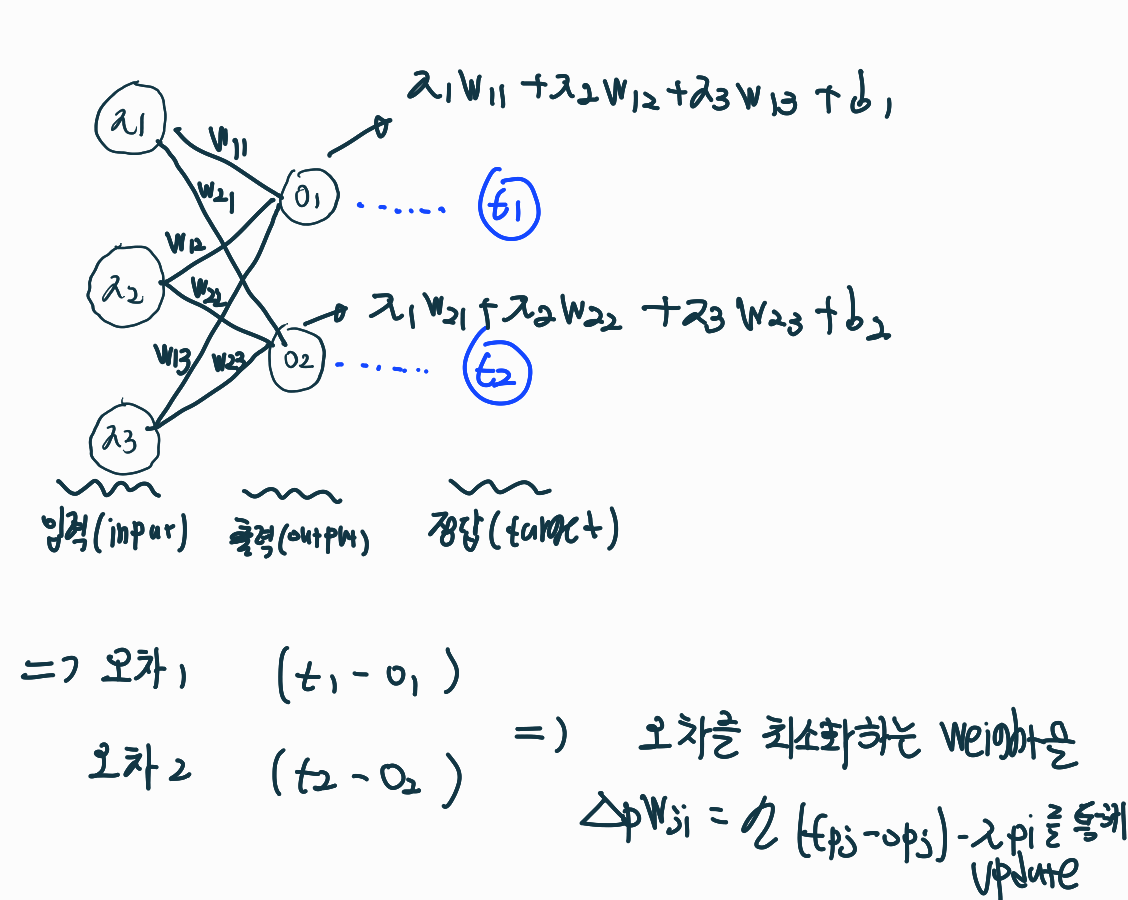
Delta Rule
\begin{equation}
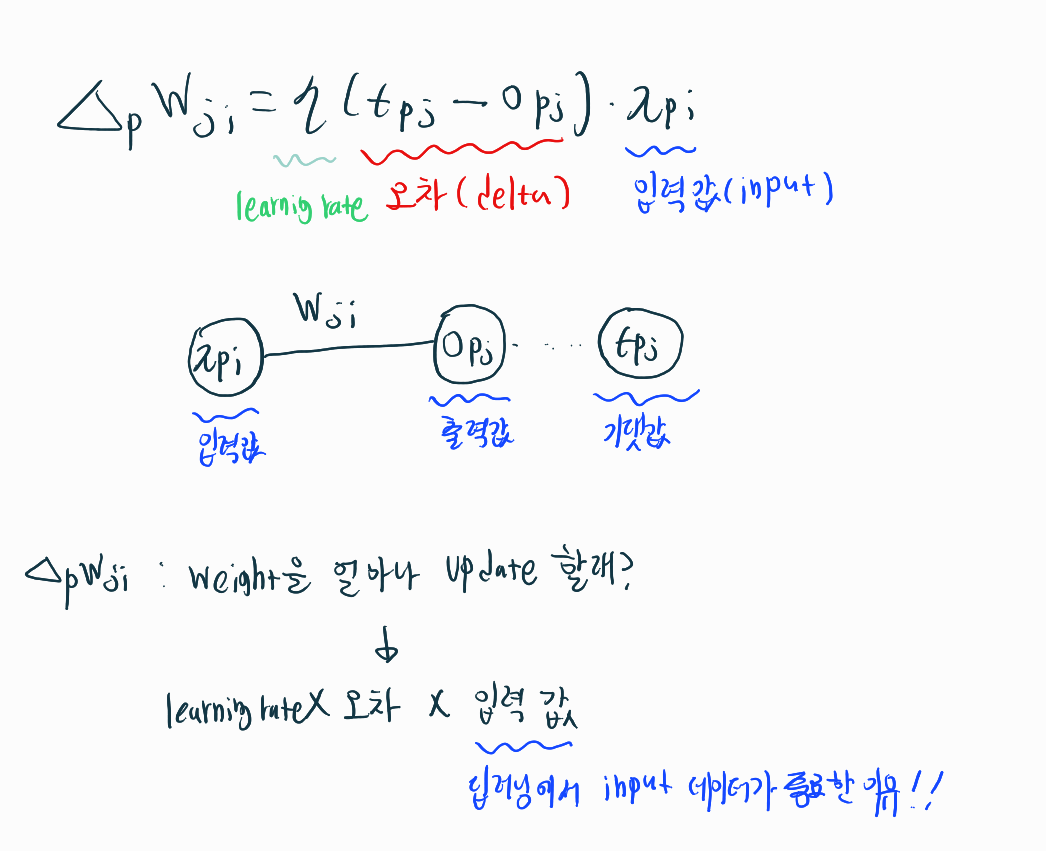
\Delta_{p} W_{j i}=\eta\left(t_{p j}-o_{p_{j}}\right) \cdot x_{p i}
\end{equation}
i는 입력 뉴런의 인덱스, j는 출력 뉴런의 인덱스, p는 샘플 인덱스
위 식을 Delta Rule이라고 하는데, 여기서 Delta는 정답값과 출력 값의 차이이다.
이 Rule은 참 단순하다. Weight의 변화량을 결정하는데 정답과 출력값이 많이 틀리면 많이 Weight을 업데이트하고, 적게 틀리면 적게 Weight을 업데이트하는 것이다. 즉, 오차에 비례하여 Weight를 업데이트한다.
Weight의 변화량을 결정하는 Delta Rule에 있어서 입력값이 곱해진다. 왜 딥러닝에서 input data가 학습에 지대한 영향을 미치는지 알 수 있는 대목이다. 따라서 우리는 입력값 Normalization과 같은 테크닉을 활용한다.
Delta Rule과 Gradient Descent
Delta Rule은 Error Function(E) 내에서 경사 하강법이다.
우리는 딥러닝에서 흔히 Error Function(Loss function)을 정의하고, 경사 하강법을 통해서 Loss가 가장 적은 Weight을 결정한다. 사실 우리가 자주 활용해온 이 경사 하강법은 위에서 배운 Delta Rule과 똑같다.
"델타 규칙에 의해 Weight의 변화가 Weight 공간상에 주어지는 오차의 제곱을 높이로 하는 곡면에 대하여 경사 하강을 한다. 즉, 오차의 제곱이 가장 많이 감소하는 방향으로 변화한다. "
\begin{equation}
o(\vec{x})=\vec{w} \cdot \vec{x}
\end{equation}
출력 값(Output)이 위와 같은 결괏값을 낸다고 했을 때, Error Function을 흔히 사용하는 Mean Squared Error(MSE)로 아래와 같이 표현할 수 있다. 1/2을 식 앞에 곱해주는 것은 미분하였을 때 2를 상쇄시키기 위한 것이다.
\begin{equation}
\begin{aligned}
&E=\sum_{p} E_{p} \\
&E_{p}=\frac{1}{2} \sum_{j}\left(t_{p j}-o_{p j}\right)^{2}
\end{aligned}
\end{equation}
위 함수에서 존재할 수 있는 모든 Weight에 대한 Error 값을 그래프로 나타내면 2차 함수 형태의 아래와 같으며,Loss Function의 형태가 Convex function의 형태로 나온다. 따라서 다른 local minimum이 존재하지 않기 때문에, Gradient descent를 활용할 수 있으며 오차의 제곱이 가장 많이 감소하는 방향으로 변화하기 위해서 미분을 활용한다.
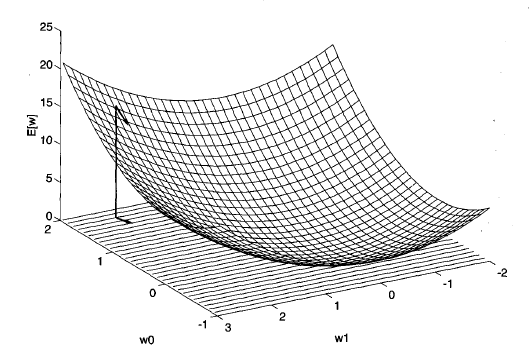
(Gradient Desent 만큼 Weight 값을 업데이트 해주며 Loss를 줄여나간다)
\begin{equation}
\Delta w_{i}=- \frac{\partial E}{\partial w_{i}}
\end{equation}
델타 규칙이 위에서 정의한 Error function(E) 내에서 경사 하강법임을 알아보기 위해 아래식이 성립함을 확인해보자
\begin{equation}
\begin{aligned}
&\left(t_{p j}-o_{p_{j}}\right) \cdot x_{p i} =\delta_{p_{j}} x_{p_{i}}(\text { DeltaRule })
\end{aligned}
\end{equation}
\begin{equation}
-\frac{\partial E_{p}}{\partial W_{j i}}(GradientDecent)=\delta_{p_{j}} x_{p_{i}}(Delta Rule)
\end{equation}
(1) E_p(error Function)은 t_p와 o_p에 대한 함수이므로, w_ji에 대해 바로 미분이 불가하기 때문에 Chain Rule을 활용해서 E_p항을 o_pj로 미분하고, o_pj를 W_ji로 미분할 것이다.
\begin{equation}
-\frac{\partial E_{p}}{\partial W_{j_{i}}}=-\frac{\partial E_{p}}{\partial O_{p_{j}}} \times \frac{\partial O_{p_{i}}}{\partial W_{j i}}
\end{equation}
(2) 첫번째, E_p를 o_pj로 편미분해보도록 하자. 그럼 o_pj를 제외한 것은 다 상수임. 식을 전개하면 정답과 출력의 차이인 Delta*(-1) 가 나옴
\begin{equation}
\begin{aligned}
\frac{\partial E_{p}}{\partial O_{p_{j}}} &=\frac{\partial\left(\frac{1}{2} \sum_{j=1}\left(t_{p_{j}}-O_{p_{j}}\right)^{2}\right)}{\partial O_{p_{j}}} \\
&=\frac{1}{2} \times 2 \times\left(t_{p_{j}}-O_{p_{j}}\right)(-1) \\
&=-\left(t_{p_{j}}-O_{p_{j}}\right)=-\delta p_{j}
\end{aligned}
\end{equation}
(2) 두번째, o_pj를 w_ji로 편미분해보도록 하자. 그럼 w_ji를 제외한 것은 다 상수임. 따라서 x_pi만 남게 된다.
\begin{equation}
\begin{aligned}
\frac{\partial o_{p j}}{\partial W_{j i}} &=\frac{\partial\left(\sum_{i=1} W_{j i} x_{p i}\right)}{\partial W_{j i}} \\
&=\frac{\partial\left(W_{j,} x_{p j}+W_{j 2} x_{p 2}+\cdots W_{j i} x_{p i}+\cdots\right)}{\partial W_{j i}} \\
&=x_{p i}
\end{aligned}
\end{equation}
(3) 즉, 가중치 업데이트양은 Delta와 입력값의 곱임을 확인할 수 있으며, 델타 규칙은 경사하강법과 같다.
\begin{equation}
\begin{aligned}
-\frac{\partial E_{p}}{\partial w_{5 i}} &=\frac{\partial E_{p}}{\partial O_{p j}} \times \frac{\partial O_{p j}}{\partial w_{j i}} \\
&=-\left(-\delta_{p j} x p_{i}\right)=\delta_{p j} x_{p i}
\end{aligned}
\end{equation}
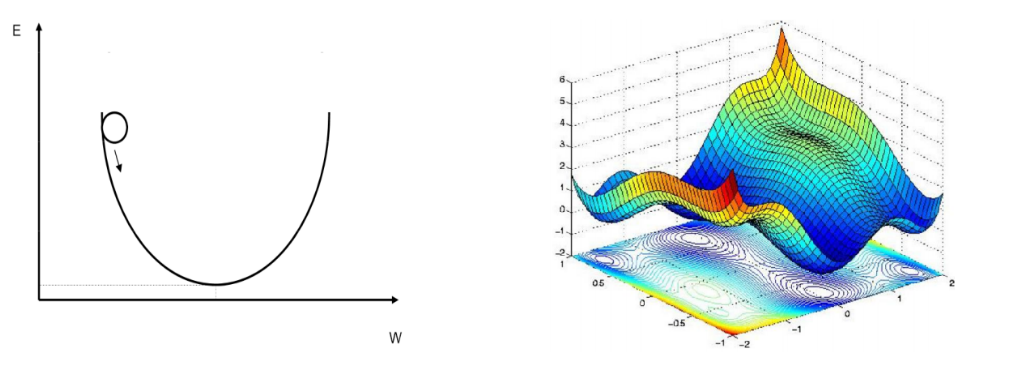
Delta Rule과 Non-Convex Function
위에서 정의한 Delta Rule은 "Hidden layer는 없이 input layer와 output layer로만 구성되어 있으며, Linear activation function만을 활용한 하나의 신경망" 이라는 아주 기초적인 조건에서만 성립한다.
하지만 우리가 앞으로 학습해야할 뉴럴 네트워크는 다음 3가지 조건을 갖추고 있을 것이다.
1. input layer, output layer 외에 깊은 Hidden layer가 존재
2. Linear activation function 말고, 비선형적인 활성화 함수(e.g, ReLu)를 활용
3. Loss Function은 Global minimum이 하나만 존재하지 않는 Non-convex Function의 형태
따라서 위에서 가정한 Delta Rule은 하나의 Local minumum을 가지고 있는 Convex 형태를 하고 있었지만, 우리가 앞으로 학습해야할 네트워크는 복잡한 non-convex Function이기 때문에 Local minimum에 수렴할 가능성이 존재한다. 따라서 Delta Rule을 변형하여 일반화하는 과정이 필요함
'블로그 > 딥러닝' 카테고리의 다른 글
| [RAG] RAG 성능 향상을 위한 Re-ranking (1) | 2024.07.11 |
|---|---|
| 딥러닝의 과대적합(Overfitting)을 해결하자 (0) | 2023.04.24 |
| 단층에서부터 Deep한 다층 퍼셉트론까지(Universal Approximation Theorem) (0) | 2022.08.13 |
| [이상치 탐지] 금형 센서 데이터 이상 탐지 사례 (0) | 2022.07.06 |
| MLE(Maximum Likelihood Estimation), 음의 로그우도(Negative log-likelihood) (0) | 2022.06.30 |



