다양한 실험에 따르면 노드 수가 많은 단층 구조 신경망보다, 비선형 함수를 활용한 노드 수가 적은 다층 구조 신경망이 훨씬 우수한 경우가 많다고 한다.
그렇다면 왜 비선형 활성화 함수(e.g., ReLu)를 활용해야 하는가? 이 이야기를 하기 전에, 우리가 어떻게 매우 복잡한 문제를 딥러닝으로 해결할 수 있는지에 대한 단서인 Universal Approxiamtion Theorem을 알아보자.
Universal Approxiamtion Theorem
Every continuous function that maps intervals of real numbers to some output interval of real numbers can be approximated arbitrarily closely by a multi-layer perceptron with just one hidden layer(with non-linear activation functions)
하나의 은닉층과 비선형 활성화 함수를 갖는 인공신경망은 임의의 연속인 다변수 함수를 원하는 정도의 정확도로 근사할 수 있다.

Universal Approximation Theorem에 따르면 아무리 복잡한 몇십 차원의 함수라도 하나의 히든 레이어와 비선형 활성화 함수를 가지고 있는 신경망으로 근사할 수 있기 때문에, 우리가 해결하고자 하는 복잡한 문제를 신경망 문제로 바꾸어서 해결할 수 있다.
그렇다면, 선형 연산으로는 불가능한가? 선형 연산의 퍼셉트론을 다층으로 쌓으면 비슷한 문제를 해결할 수 있지 않을까?
그렇지 않다.
이는 선형 처리는 아무리 여러 단계를 반복해도 하나의 선형 처리로 줄여 표현할 수 있다는 수학적 원리 때문이다.
곱셉과 덧셈으로만 이루어지는 선형 연상의 특성상 항상 입력의 일차 함수로 나타난다. 즉, 단순 퍼셉트론으로는 우리가 해결해야 하는 Non-convex 함수와 같은 복잡한 함수를 제대로 학습하지 못한다는 결론에 이르게 된다.
따라서, Universal Approximation Theorem과 같이 하나의 히든 레이어와 비선형 활성화 함수를 추가하면 입력의 일차 함수 표현을 넘어서 다양하고 복잡한 형태의 출력을 만들 수 있으며, 복잡한 함수를 표현할 수 있게 되는 것이다.
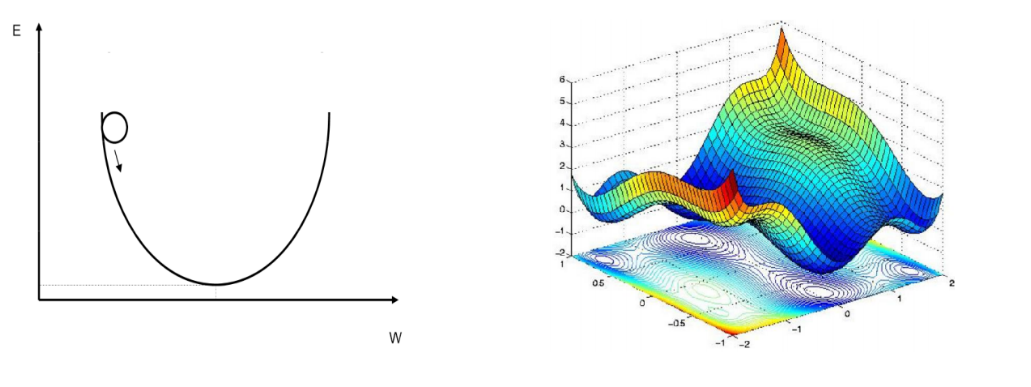
비선형 활성화 함수를 갖춘 히든 레이어를 충분한 수의 퍼셉트론으로 구성한다면 어떠한 어려운 함수도 근사할 수 있는 것을 알 수 있었다.
하지만, 딥러닝으로 풀어야 하는 문제가 복잡하다면 히든 레이어에 필요한 퍼셉트론의 수가 늘어날 수 있으며, Universal Approximation Theorem에서 가정한 하나의 히든 레이어와 비선형 활성화 함수로는 입력 데이터로부터 유용한 정보를 추출해낼 수 없다. 이러한 이유로 신경망에 여러 개의 히든 레이어를 쌓으려고 하는 것이며, 딥(Deep)한 다층 퍼셉트론이 부각된 것이다.
정리하자면, 하나의 히든 레이어와 비선형 활성화 함수로 모든 복잡한 함수에 근사할 수 있다. 하지만 입력 데이터로부터 유용한 정보를 추출하기 위해 여러 개의 히든 레이어를 쌓은 다층 퍼셉트론(MLP)이 등장하였으며, 보다 딥(Deep)한 모델이 필요한 것이다.
추가로 딥(Deep)한 다층 퍼셉트론 모델은 많은 계산량과 적은 데이터 수로부터 적절한 파라미터를 학습시키지 못한다는 단점도 있다. 따라서 입력 데이터로부터 유용한 정보를 효과적으로 추출하여 적절한 파라미터를 학습시키기 위해 다양한 딥러닝 아키텍처가 발전했으며, 이미지 학습에 효과적인 CNN, Sequential 한 정보를 반영하는 RNN, LSTM 등의 딥러닝 아키텍처가 등장한 것이다.
예를 들어, 이미지를 분류할 때 다층 퍼셉트론 신경망(MLP)는 픽셀을 1차원으로 펴줘야 하기 때문에 많은 파라미터 수가 발생하는데도 그 결과가 local connected 하는 CNN에 비해 떨어진다.
이렇게 만들어진 다양한 딥러닝 아키텍처가 여러 분야에서 우수한 성능을 보이고 있다고 해도, 왜 이런 우수한 성능이 얻어질 수 있는지는 아직까지 수학적으로 증명된 것은 아니라고 한다.
현업에서 데이터를 다룬다는 것은 항상 누군가를 설득하는 자리기에, 모델의 성능 결과를 합리적으로 설명할 수 있어야 한다. 최근에는 설명 가능한 AI, XAI(eXplainable Artificial Intelligence)라는 딥러닝 영역이 계속해서 발전하고 있는 것도 이러한 차이에서 부터 오는 것이지 않을까 한다. 딥러닝을 학습하고 있는 입장으로서 언젠가는 현업에서 문제 해결을 위해 거침없이 딥러닝 아키텍처를 활용할 수 있는 날이 올 수 있으면 좋겠다.
Reference:
파이썬 날코딩으로 알고짜는 딥러닝, 윤덕호
'블로그 > 딥러닝' 카테고리의 다른 글
| [RAG] RAG 성능 향상을 위한 Re-ranking (1) | 2024.07.11 |
|---|---|
| 딥러닝의 과대적합(Overfitting)을 해결하자 (0) | 2023.04.24 |
| [이상치 탐지] 금형 센서 데이터 이상 탐지 사례 (0) | 2022.07.06 |
| 역전파 알고리즘(Back Propagation)과 Delta Rule(1) (0) | 2022.07.06 |
| MLE(Maximum Likelihood Estimation), 음의 로그우도(Negative log-likelihood) (0) | 2022.06.30 |



